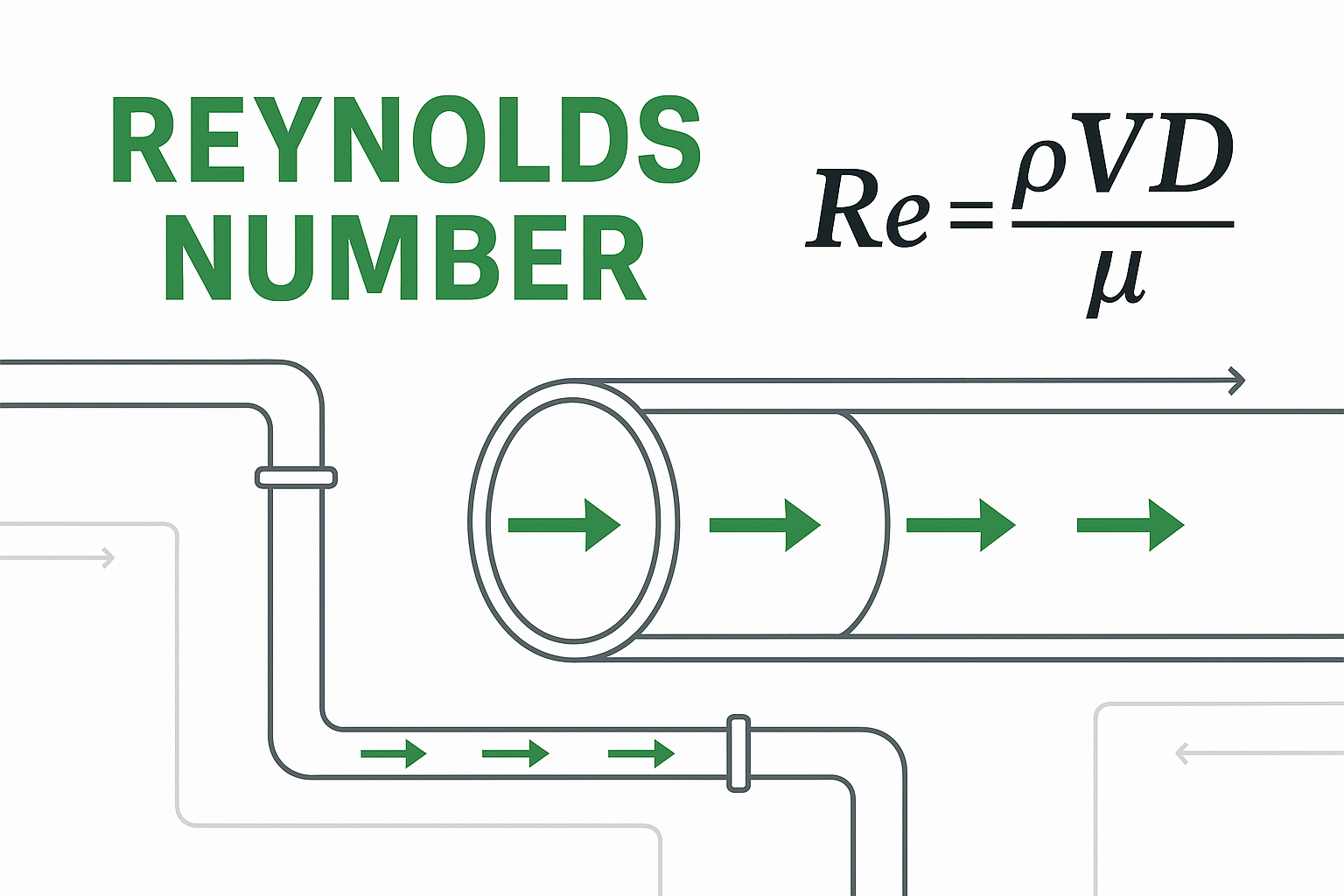
Reynolds Number (Re) is a fundamental concept in fluid mechanics that helps engineers and scientists understand the nature of fluid flow. It is a dimensionless quantity used to predict flow patterns in different fluid flow situations. Named after Osborne Reynolds, who first studied its effects in the late 19th century, this number is crucial in designing pipelines, aircraft, automobiles, and many other engineering applications.
Reynolds Number Calculator
What is Reynolds Number?
Reynolds Number (Re) is defined as the ratio of inertial forces to viscous forces in a fluid. It determines whether the fluid flow is laminar, turbulent, or in a transitional phase.
Mathematical Formula:
Where:
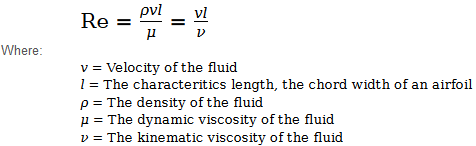
Understanding Flow Regimes
The Reynolds Number helps categorize fluid flow into three main regimes:
- Laminar Flow (Re < 2,000):
- Fluid moves in smooth, parallel layers with minimal mixing.
- Common in low-velocity flows and highly viscous fluids.
- Example: Flow of honey, slow-moving water in pipes.
- Transitional Flow (2,000 < Re < 4,000):
- Flow shows characteristics of both laminar and turbulent flow.
- This regime is unstable and can switch between laminar and turbulent.
- Example: Water flowing in a pipe at an intermediate velocity.
- Turbulent Flow (Re > 4,000):
- Fluid motion is chaotic with eddies and vortices.
- Occurs at high velocities or low-viscosity fluids.
- Example: Water flowing out of a tap at high speed, airflow over an aircraft wing.
Importance of Reynolds Number in Engineering
- Pipe Flow Analysis: Engineers use Re to determine pressure drops, pipe sizing, and pumping requirements.
- Aerodynamics: Aircraft and car designers use it to predict drag and optimize shapes for efficiency.
- Heat Exchangers: Helps in designing efficient cooling and heating systems by determining flow behavior.
- Marine Engineering: Predicts fluid behavior around ships, submarines, and underwater structures.
Real-World Examples
- Blood Flow in Arteries: The Reynolds Number is used in biomedical engineering to study blood circulation and detect abnormalities.
- Design of Wind Tunnels: Engineers use scaled models and match Reynolds Numbers to real-life conditions to study aerodynamics.
- Weather Systems: Atmospheric scientists use Reynolds Number to study wind flow and predict weather patterns.
How to Calculate Reynolds Number
Example Problem:
Given:
- Water at 20°C with and .
- Flow velocity = 2 m/s
- Pipe diameter = 0.05 m
Solution: Since , the flow is turbulent.