Mohr’s circle calculator

Professor
Calculators

Mohr’s Circle Calculator

Visualize & Calculate Stress Transformations in 5 Minutes

Struggling to determine principal stresses or maximum shear stress in your mechanics class or design project? Mohr’s Circle is a powerful graphical and computational tool that transforms complex stress analysis into visual clarity. Our interactive calculator provides instant results with visual circle representation, making stress transformation analysis accessible for students, engineers, and designers alike.

Start Calculating Now Learn the Theory
Instant Calculations
Visual Circle Plot
Downloadable Results
Student-Friendly

Why Mohr’s Circle Matters for Mechanical Engineers

Mohr’s Circle is a graphical representation of the stress transformation equations at a point within a material. Named after German civil engineer Christian Otto Mohr, this elegant geometric construction converts algebraic stress transformation equations into an intuitive visual format that reveals critical information about stress states at any orientation.

Rather than solving trigonometric equations repeatedly for different angles, Mohr’s Circle allows engineers to visualize all possible stress states on a material element simultaneously. Every point on the circle represents the normal and shear stress on a plane at a specific orientation—making it an indispensable tool for stress analysis.

Design Applications

Determine principal stresses for evaluating failure criteria in machine elements, pressure vessels, and structural components. Identify critical stress states that govern yielding, fracture, or fatigue life.

Stress Transformation

Calculate normal and shear stresses on any oriented plane without complex trigonometric calculations. Essential for analyzing welds, joints, and inclined sections in structural analysis.

Failure Analysis

Identify maximum shear stress planes for ductile material failure prediction and principal stress planes for brittle fracture assessment. Critical for safe design of mechanical systems.

Academic Excellence

Master mechanics of materials coursework by visualizing abstract concepts. Verify hand calculations, check homework solutions, and develop intuitive understanding of stress behavior.

Real-World Engineering Impact

From designing shafts subjected to combined bending and torsion to analyzing welded joints under complex loading, Mohr’s Circle bridges theoretical mechanics and practical engineering. It supports students mastering fundamental concepts while providing working engineers with rapid stress analysis capabilities essential for design validation, failure investigation, and finite element analysis verification.

Theory & Underlying Concepts

Stress Components & Coordinate Systems

Understanding stress components is fundamental to applying Mohr’s Circle. Consider a small material element subjected to forces creating internal stresses. These stresses act on the element’s faces and are characterized by:

Normal Stresses (σ)

Stresses acting perpendicular to the face of an element. Denoted as σₓ (acting in x-direction on x-face) and σᵧ (acting in y-direction on y-face).

  • Tensile stress: Positive sign convention—material is being pulled apart
  • Compressive stress: Negative sign convention—material is being squeezed

Shear Stresses (τ)

Stresses acting parallel to the face of an element, creating a sliding or shearing action. Denoted as τₓᵧ (acts on x-face in y-direction) and τᵧₓ (acts on y-face in x-direction).

  • Complementary shear: For equilibrium, τₓᵧ = τᵧₓ in magnitude
  • Sign convention: Positive when creating clockwise rotation on the element
Critical Sign Convention: In Mohr’s Circle construction, shear stress causing counterclockwise rotation of the element is plotted upward (positive), while clockwise rotation is plotted downward (negative). This convention differs from some textbooks—always verify which convention your course or design standard uses.

Stress Transformation Equations

When a material element is rotated by an angle θ from the original x-y coordinate system, the stress components on the new faces change. The transformation equations relate original stresses to stresses on the rotated element:

Normal Stress on Rotated Plane:

σₙ = (σₓ + σᵧ)/2 + (σₓ – σᵧ)/2 · cos(2θ) + τₓᵧ · sin(2θ)

Shear Stress on Rotated Plane:

τₙ = -(σₓ – σᵧ)/2 · sin(2θ) + τₓᵧ · cos(2θ)

Understanding the Variables

  • θ (theta): Rotation angle of the element measured counterclockwise from the x-axis
  • 2θ (two-theta): Appears in equations due to double-angle trigonometric identities—this is why angles on Mohr’s Circle are doubled
  • σₙ: Normal stress on the rotated plane
  • τₙ: Shear stress on the rotated plane
The Power of Mohr’s Circle: Rather than solving these equations for every angle θ, Mohr’s Circle plots all solutions simultaneously. Each point on the circle represents (σₙ, τₙ) at a specific orientation, allowing you to read stress values directly from the geometric construction.

Constructing Mohr’s Circle: Step-by-Step

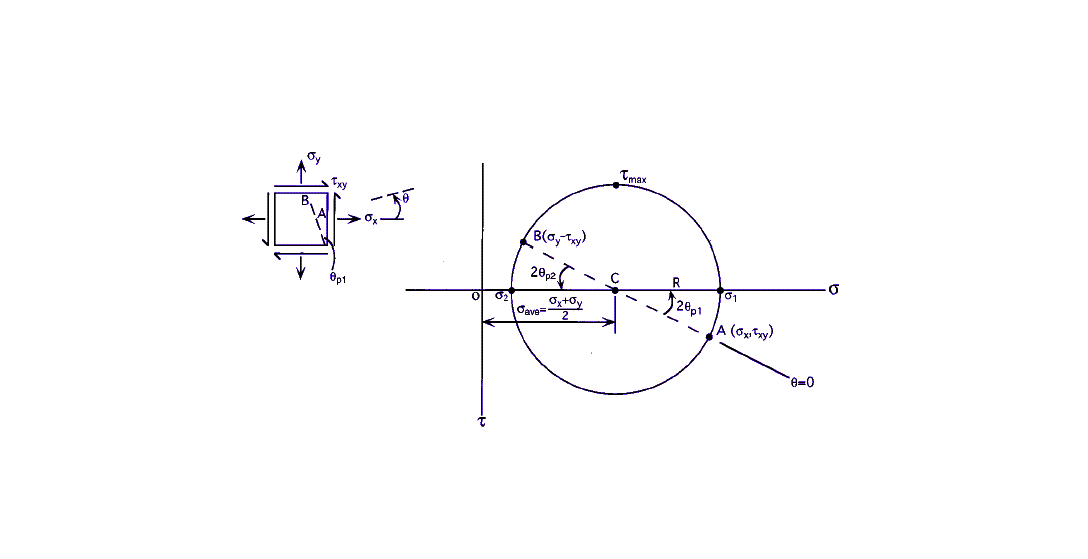
Mohr’s Circle is constructed in stress space where the horizontal axis represents normal stress (σ) and the vertical axis represents shear stress (τ). Follow these systematic steps:

1

Plot the Initial Stress Points

Plot point A with coordinates (σₓ, τₓᵧ) representing the stress state on the x-face of the original element.

Plot point B with coordinates (σᵧ, -τₓᵧ) representing the stress state on the y-face. Note the negative sign on shear stress for the y-face.

2

Determine the Circle Center

The center C of Mohr’s Circle lies on the σ-axis (where τ = 0) at:

σavg = (σₓ + σᵧ) / 2

This represents the average normal stress, which remains constant regardless of element orientation—an invariant property of the stress state.

3

Calculate the Circle Radius

The radius R is the distance from the center to either point A or B:

R = √[((σₓ – σᵧ)/2)² + τₓᵧ²]

This radius equals the maximum shear stress that can occur at any orientation of the element.

4

Draw the Complete Circle

Using center C and radius R, draw the complete circle. Every point on this circle represents a valid stress state at some angle θ. The circle encompasses all possible combinations of normal and shear stress for the given loading condition.

Important Geometric Properties

  • Points A and B are diametrically opposite on the circle, representing perpendicular faces
  • Moving around the circle by angle 2θ corresponds to rotating the element by angle θ
  • The circle always intersects the σ-axis at two points—these are the principal stresses
  • The topmost and bottommost points of the circle represent maximum shear stress states

Finding Principal Stresses & Maximum Shear Stress

The most valuable information extracted from Mohr’s Circle includes the principal stresses and maximum shear stress—critical values for failure analysis and design optimization.

Principal Stresses

Principal stresses are the maximum and minimum normal stresses that occur at specific orientations where shear stress equals zero. These planes are called principal planes.

Maximum Principal Stress (σ₁)
σ₁ = σavg + R = (σₓ + σᵧ)/2 + √[((σₓ – σᵧ)/2)² + τₓᵧ²]

The rightmost point where the circle intersects the σ-axis.

Minimum Principal Stress (σ₂)
σ₂ = σavg – R = (σₓ + σᵧ)/2 – √[((σₓ – σᵧ)/2)² + τₓᵧ²]

The leftmost point where the circle intersects the σ-axis.

Principal Plane Orientation

The angle to the principal planes from the x-axis is:

tan(2θp) = 2τₓᵧ / (σₓ – σᵧ)

This equation yields two angles 90° apart, corresponding to the two principal planes. Remember: the angle on the circle is 2θ, so divide by 2 to get the actual element rotation angle θp.

Maximum Shear Stress

Maximum shear stress occurs at planes oriented 45° from the principal planes. This value is critical for ductile material failure prediction using the Tresca yield criterion.

Maximum In-Plane Shear Stress
τmax = R = √[((σₓ – σᵧ)/2)² + τₓᵧ²]

Equals the radius of Mohr’s Circle. Found at the highest and lowest points on the circle.

Maximum Shear Plane Orientation

The planes of maximum shear stress are oriented at θs = θp ± 45° from the x-axis. On Mohr’s Circle, these points are 90° from the principal stress points.

Normal Stress on Maximum Shear Planes

Importantly, planes of maximum shear stress are not stress-free. They experience normal stress equal to the average normal stress:

σ = σavg = (σₓ + σᵧ) / 2
Design Significance: For ductile materials (like steel), yielding initiates when maximum shear stress reaches a critical value. For brittle materials (like cast iron), fracture occurs when maximum principal stress (or minimum, if highly compressive) exceeds material strength. Mohr’s Circle instantly reveals both failure modes.

Extension to 3-D Stress States

While our calculator focuses on plane stress (2-D) for accessibility, real engineering components often experience three-dimensional stress states with three principal stresses: σ₁, σ₂, and σ₃.

Mohr’s Circles for 3-D Stress

A complete 3-D stress state requires three Mohr’s Circles:

  • Large circle: Between σ₁ (maximum) and σ₃ (minimum principal stresses)
  • Medium circle: Between σ₁ and σ₂
  • Small circle: Between σ₂ and σ₃

The absolute maximum shear stress is the radius of the largest circle:

τabs-max = (σ₁ – σ₃) / 2
Plane Stress Simplification: When one principal stress is zero (common in thin plates, free surfaces, or shells), we have plane stress conditions. This 2-D simplification covers most undergraduate coursework and many practical engineering scenarios, making it an excellent starting point for mastering stress analysis.

Advanced Mohr’s Circle Calculator

Professional stress transformation analysis with interactive visualization

Input Parameters

MPa
MPa
MPa

Display Options

Try Example Problems

Conceptual Understanding: Beyond the Math

True mastery of Mohr’s Circle transcends memorizing formulas. Understanding the why behind the geometry transforms this from a calculation technique into engineering intuition that guides design decisions.

Visualizing Stress Transformation

Imagine a tiny cube of material experiencing stress. As you mentally rotate this cube, the normal and shear stresses on its faces change continuously. Mohr’s Circle captures this entire transformation in a single elegant plot.

The Circle as a Stress “Map”

Every point on Mohr’s Circle corresponds to a specific orientation of your material element:

  • Moving counterclockwise around the circle = rotating the element counterclockwise in physical space
  • Horizontal distance from the origin = normal stress magnitude
  • Vertical distance from the σ-axis = shear stress magnitude
  • Complete circuit (360°) on circle = 180° physical rotation (element returns to same stress state)
Aha moment: The circle doesn’t show stress distribution in space—it shows how stresses at a single point vary with orientation. This is fundamentally different from stress contour plots in FEA, which show spatial variation.

Interpreting the Circle Geometrically

The Diameter

The line connecting points A and B (original x and y faces) is always a diameter of the circle. This geometrically represents that these faces are perpendicular—diametrically opposite orientations on the circle.

Implication: Perpendicular planes always appear as opposite ends of a diameter. This makes finding stresses on perpendicular faces trivial—just go to the other end of the diameter.

Circle Intersections with σ-Axis

Where the circle crosses the horizontal axis, shear stress is zero. These are the principal stress points by definition. The circle must cross the σ-axis twice (or touch it twice if it’s tangent), giving two principal values.

Implication: At every point in a stressed material, there always exist two mutually perpendicular planes with zero shear stress. These principal planes are nature’s “preferred” directions at that point.

Maximum Vertical Distance

The highest and lowest points on the circle (maximum τ coordinate) represent planes of maximum shear stress. These occur at 45° from the principal planes in physical space (90° on the circle).

Implication: Maximum shear always occurs on planes oriented 45° from principal planes. This explains why ductile materials (which fail in shear) often show 45° slip lines, while brittle materials (which fail in tension) crack perpendicular to maximum principal stress.

The Center Point

The circle’s center at (σavg, 0) represents an invariant—a value that doesn’t change regardless of element orientation. This average normal stress is a fundamental property of the stress state at that point.

Implication: Hydrostatic pressure (equal stress in all directions) cannot be transformed away by rotation. It’s an intrinsic property of the loading condition, not the coordinate system choice.

Relating to Real Material Behavior

Mohr’s Circle isn’t abstract mathematics—it directly predicts how real materials will behave and fail under complex loading.

Ductile vs. Brittle Failure Modes

Ductile Materials (Steel, Aluminum, Copper)

Ductile materials fail through plastic deformation driven by shear stress. Atoms slide past each other along slip planes oriented for maximum shear.

Mohr’s Circle prediction: Look at τmax (circle radius). When this reaches roughly σyield/2, plastic yielding begins. The material will deform permanently on planes at 45° from principal stress directions.

Real example: Pull a steel tensile specimen until it yields. It will neck down at 45° angles—maximum shear planes—forming a “cup and cone” fracture with visible slip bands.

Brittle Materials (Cast Iron, Concrete, Ceramics)

Brittle materials fail through crack propagation driven by normal stress. Atomic bonds break under tension, creating fractures perpendicular to the loading direction.

Mohr’s Circle prediction: Look at σ₁ (maximum principal stress). When this reaches σultimate-tension, cracks initiate perpendicular to σ₁ direction—the principal plane experiencing maximum tension.

Real example: Twist a piece of chalk. Even though you’re applying pure torsion (shear), it breaks at 45° angles. Why? Mohr’s Circle shows pure shear creates principal tensile stress at 45°, and chalk fails in tension, not shear.

Why Maximum Stresses Matter for Design

Engineers don’t just need to know that a component is stressed—they need to know the maximum stress and where it occurs. Mohr’s Circle provides both:

  • Magnitude: σ₁, σ₂, and τmax tell you how severe the stress is
  • Location: θₚ and θₛ tell you on which planes these maxima occur
  • Failure mode: The relative magnitudes guide material selection and failure analysis

This information is critical for:

  • Determining adequate safety factors
  • Selecting appropriate materials (ductile vs. brittle failure considerations)
  • Identifying likely crack initiation sites for fracture mechanics
  • Optimizing orientation of fibers in composites or grain structure in forgings

Common Conceptual Mistakes

Mistake: “Mohr’s Circle shows stress distribution across the part”

Reality: Mohr’s Circle shows stress transformation at a single point, not spatial distribution. Every point in a stressed body has its own Mohr’s Circle (potentially different). FEA contour plots show spatial distribution; Mohr’s Circle shows orientation dependence at one location.

Mistake: “The shear stress on Mohr’s Circle is actual shear on the material”

Reality: The vertical coordinate represents shear stress on faces at various orientations, not shear as a vector quantity. The sign convention (which direction is positive) is purely for constructing the circle correctly—it doesn’t directly indicate shear direction in space.

Mistake: “Larger circle always means worse stress state”

Reality: Circle size indicates stress range and maximum shear, but danger depends on material properties. A large circle with moderate stresses in strong steel may be perfectly safe, while a small circle with high average stress in brittle ceramic could be catastrophic. Compare circle values to material strengths, not absolute circle size.

Mistake: “Principal stresses are always the applied stresses”

Reality: Principal stresses often differ significantly from applied stresses, especially when shear is present. You must calculate them using Mohr’s Circle. Applied stress components (σₓ, σᵧ, τₓᵧ) are in an arbitrary coordinate system; principal stresses are in the material’s “natural” coordinate system for that stress state.

Mistake: “The angle on the circle is the physical angle”

Reality: Always remember the 2θ rule! An angle of 60° measured on Mohr’s Circle corresponds to 30° physical rotation of the element. This factor of 2 comes from the trigonometric derivation and trips up countless students on exams. When reading angles off the circle, divide by 2.

Building Intuition Through Examples

The best way to internalize Mohr’s Circle is through mental models and physical analogies:

The Rotating Cube Mental Model

Imagine holding a tiny stressed cube. As you rotate it, you’re not changing the internal forces— you’re just viewing them from different angles. Mohr’s Circle is like a “map” showing what you’d measure at every rotation angle.

The beauty? You don’t need to rotate it infinitely many times. Draw the circle once, and you’ve captured all possible orientations simultaneously.

The Tension-Shear Equivalence

Pure shear and combined tension-compression are the same stress state, just viewed differently. A circle centered at the origin (pure shear) shows equal principal stresses in tension and compression. This explains why shear failures often look like tensile failures at 45°.

Try it: Twist a rectangular eraser. It fails at 45° angles—not because shear is strongest there, but because tension is strongest there!

The Zero-Shear Rule

Every stressed point has exactly two special orientations where shear stress vanishes completely— the principal planes. No matter how complex the loading, these exist. This is a fundamental theorem of stress analysis, proven geometrically by the circle intersecting the σ-axis.

Engineers exploit this: aligning components with principal stress directions minimizes shear-driven failures like delamination in composites or slip in crystals.

Summary & Key Takeaways

Mohr’s Circle transforms the abstract mathematics of stress transformation into visual, intuitive understanding. Master this tool, and you’ve unlocked a cornerstone of mechanical design, failure analysis, and materials science.

What is Mohr’s Circle?

A graphical representation that shows all possible stress states at a point as you rotate the coordinate system. Every point on the circle represents (σₙ, τₙ) for a specific orientation angle θ.

How to Construct It

Plot points A(σₓ, τₓᵧ) and B(σᵧ, -τₓᵧ), find the center at σavg = (σₓ + σᵧ)/2, calculate radius R = √[((σₓ – σᵧ)/2)² + τₓᵧ²], and draw the circle through these points.

Key Values It Reveals

Principal stresses: σ₁ and σ₂ at circle-σ axis intersections
Maximum shear: τmax = circle radius
Orientations: θₚ and θₛ from geometric angles (remember 2θ rule!)

Engineering Applications

Essential for shaft design, pressure vessel analysis, weld evaluation, failure theory application, FEA verification, and understanding material behavior under complex loading.

Critical Reminders

Angles on circle are 2θ (double actual rotation). Sign conventions matter but don’t change principal stresses. Every point in a body has its own circle. Always verify units are consistent.

Beyond Plane Stress

Extends to 3-D stress (three circles), strain analysis (same principles), and even moments of inertia. The geometric intuition applies universally to tensor transformations.

The Engineer’s Perspective

“Mohr’s Circle is more than a calculation tool—it’s a lens through which to view stress. When you can visualize the circle in your mind as you examine a component, you’ve achieved true mechanical intuition. The numbers matter, but understanding why the circle looks the way it does reveals the physics of failure and the path to better design.”

— Principles of Mechanical Design

Study Tips for Mastery

Practice drawing: Sketch circles by hand for different problems. The tactile act of drawing builds neural pathways that pure calculation doesn’t.

Verify with calculator: Always check your manual work with our calculator above. Catching errors immediately prevents reinforcing mistakes.

Visualize transformation: For each problem, imagine physically rotating the element and how stresses change. Make it tangible, not abstract.

Connect to failure: Always relate results to failure modes. Ask “would this fail?” and “how would it fail?” Connect theory to reality.

References & Further Reading

Textbooks & Academic Resources

  • Beer, F. P., Johnston, E. R., DeWolf, J. T., & Mazurek, D. F. (2020). Mechanics of Materials (8th ed.). McGraw-Hill Education. Classic textbook with comprehensive Mohr’s Circle coverage and examples
  • Hibbeler, R. C. (2017). Mechanics of Materials (10th ed.). Pearson. Excellent visual explanations and step-by-step problem solutions
  • Gere, J. M., & Goodno, B. J. (2018). Mechanics of Materials (9th ed.). Cengage Learning. In-depth theoretical treatment with engineering applications
  • Timoshenko, S. P., & Goodier, J. N. (1970). Theory of Elasticity (3rd ed.). McGraw-Hill. Advanced mathematical treatment for graduate-level study

Online Resources & Tutorials

  • MIT OpenCourseWare – Mechanics of Materials (Course 3.11) Free lecture notes, videos, and problem sets from MIT
  • eFunda Engineering Fundamentals – Mohr’s Circle Interactive tools and detailed theory explanations
  • Virginia Tech EngApplets – Mohr’s Circles for 3-D Stress Analysis Interactive Java applets for visualizing 3-D cases
  • Engineering ToolBox – Stress Analysis Resources Quick reference formulas and conversion factors

Video Lectures & Courses

  • Coursera – Mechanics of Materials Specialization Comprehensive video course series with assignments
  • Jeff Hanson – Mohr’s Circle Tutorial Series (YouTube) Clear, step-by-step video explanations for students
  • Khan Academy – Advanced Physics / Engineering Free introductory content with practice exercises

Community & Discussion Forums

  • r/EngineeringStudents (Reddit) Active community for homework help and concept clarification
  • Engineering Stack Exchange Q&A format for specific technical questions
  • Physics Forums – Engineering Systems & Design Deep technical discussions and problem-solving

Design Standards & Codes

  • ASME Boiler & Pressure Vessel Code (Section VIII) Industrial standards applying stress analysis principles
  • AISC Steel Construction Manual Structural steel design with combined stress procedures
  • API 579-1/ASME FFS-1 Fitness-For-Service Assessment procedures using principal stress concepts

Note: This calculator and guide are educational resources intended to supplement formal coursework and textbooks. For critical engineering applications, always consult applicable design codes, conduct peer review, and follow professional engineering practices. When in doubt, verify results using multiple methods and reference sources.

Ready to Master Stress Analysis?

You now have the tools, theory, and practice problems to excel in mechanics of materials. Take these next steps to solidify your understanding:

Use the Calculator

Work through your homework and verify your solutions. Build confidence through hands-on practice.

Try Calculator Now

Bookmark This Page

Save this resource for quick reference during exams, design projects, and professional work.

Share with Classmates

Help others learn by sharing this calculator. Study groups achieve better results together.

Explore More Mechanical Engineering Tools

Beam Deflection Calculator Shaft Design Tool Factor of Safety Calculator Stress-Strain Converter

Related Posts

Leave a Reply

Your email address will not be published. Required fields are marked *